One File for the Price of Three: Catching Cheating Servers in Decentralized Storage Networks

The Pitch

The world has an insatiable hunger for storage. We're using more and more storage, and we're doing it much faster than we can build more But tons of storage devices—laptop and desktop hard drives, standalone storage systems, flash memory on mobile phones, and more, and more, and more—are sitting idle.

Wouldn't it be nice if all of this unused storage could be tapped? And wouldn't it be nicer still if its owners could profit from it? We may never know why Ethan configured his desktop with 6 TB of space despite needing less than 500 GB, but given his grad student stipend, it would be great to see him get something out of it.

The Billion-Dollar Token: Decentralized Storage Networks (DSNs), such as Sia, Storj, MaidSafe, and the soon-to-be-released Filecoin, promise to do exactly this. They offer users tokens for renting out their own unused storage. Yes, you can turn your hard drive into an AirBnB for bits.

Of course, you need a mechanism to make sure users actually store what they say they are storing. This is fairly easy at least in concept: to check that someone a copy of the file, ask them for small pieces of it at random periodically.

The Billion-Dollar Problem: If you store your data with Amazon or Google or Microsoft, they promise to store your file multiple times. That way if a hard drive fails, your pictures aren't gone. Our DSN needs to do the same thing. After all, the average home computer is not reliable. To store our pictures on three computers, we need to pay each one of them, but that's a small price to pay if it makes the data safe, right? Unfortunately, you are unlikely to get what you pay for.

Once there is money involved, people take shortcuts for profits. Instead of storing one file three times at $1 per copy, a set of servers can pretend to do so and only keep one copy between all three of them. Whenever anyone checks if one of their computers has a copy, they can use the single shared copy to pass any test asked of them. As a result, they can free up space to store two more files which they also falsely claim to have replicated. This nets them 3X as much money. It also means there's only one copy of your pictures and it's probably on the least reliable computer they could find (those are cheaper, after all). The only practical way around this is to make the three copies entirely distinct.

Sia, Storj, MaidSafe, etc. do this by encrypting your pictures three times and distributing those encrypted copies. This strategy solves the problem perfectly if you're the one encrypting your photos and someone else is storing them.

The Challenge: But what happens if the data isn't your family photos? What happens if it's a public good like blockchain state? Blockchains are getting huge—Ethereum is over 75 GB and growing fast—and it's really expensive to have everyone store everything. But who encrypts the blockchain state? Everyone needs to read it. And worse, we don't trust anyone to encrypt it properly. We need something totally different that anyone can check and anyone can decode.

We need a Public Incompressible Encoding. In fact, this is needed for many settings, for example if you want some mining process that depends on miners storing arbitrary files.

Making PIEs is Hard

If anyone can decode data and we can't trust anyone to encode it properly, then how, you might ask, could we possibly prevent the attack we described above? Assume we have a malicious server, Mallory, who tries to store as little as possible. Sure, we can encode a file in three different ways, but if everything is public, our cheating storage server Mallory can still just store one copy. When we query her for an encoding, she can re-encode her one copy to whichever encoding was asked for. It seems impossible to stop.

Indeed, without secret information, we need some other way to restrict Mallory. We can do this with time. If re-encoding any piece of the file takes a few minutes, we can probably tell if we ask for the file and Mallory responds in two minutes instead of two seconds. At the same time, if we don't do the encoding piecemeal, we can make encoding an entire file reasonably efficient.

This idea isn't new. Filecoin suggested using timing, as did van Dijk et al. for some related mechanisms. So what's the problem?

Well, van Dijk et al. mix data blocks together in a configuration that makes recomputing discarded data really slow...if Mallory is pulling all of her data from the same rotational hard drive. These days that's probably not a good assumption, especially if she's cheating with custom hardware. Filecoin suggested something simpler: a long repeated chain of operations over the whole file. Unfortunately, van Dijk et al. anticipated this construction and showed that Mallory can save most of the storage and almost all of the computation by storing carefully-selected intermediate values.

So Filecoin's approach is broken and van Dijk et al. makes assumptions about hardware that no longer hold. Given the ability to build ASICs, we need to be extremely careful about what assumptions we use. Indeed, many things that were billed as ASIC resistant—such as Equihash and Ethhash—now have ASICs.

Rather than finding some new hardware assumption for storage, we build our PIE around some fairly slow key derivation function (KDF)—what non-cryptographers might refer to as a kind of hash function. For the prototype, we use scrypt, which exploits the fact that it appears hard to accelerate sequential memory access without advances in commodity RAM, but if that turns out to be false, any moderately slow KDF will do. To make things really slow, we force Mallory to run our KDF a large number of times in sequence.

This, of course, raises the all-important question: how do we force that work to be sequential? Enter graph theory.

Computation as a DAG: To understand data dependencies within our computation, we represent it as a directed acyclic graph (DAG). Each vertex represents an operation with two steps: first we derive a key using KDF, and then we encrypt some data using that key. Edges are either data edges, representing the inputs and outputs of the encryption, or key edges, representing the data used by KDF to derive the key. In the below graph red dashed edges are key edges, while solid black edges are data edges.

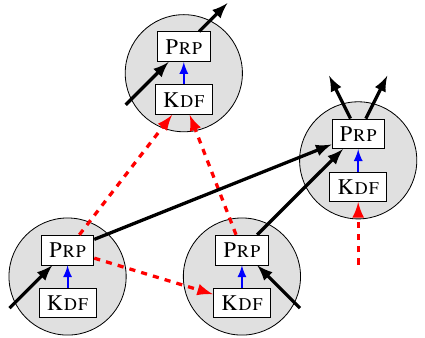
We can use this formulation to track how much sequential work needs to happen. Because we need the output from one vertex in order to compute the values at any of its children, a path in the graph corresponds to inherently sequential work. Any key edges in that path require inherently sequential calls to KDF. Therefore, if the graph has long paths of key edges, encoding will require a lot of sequential work.

But we don't just care about encoding the whole file. We need Mallory to do a lot of work even if she only throws away some of the data. Worse, Filecoin's original proposal was broken by storing intermediate values, so we need to watch out for that as well. Since every piece of data in our computation is the output of a vertex in our graph representation, we can view Mallory storing data (intermediate or not) as removing vertices from the graph. We now need to check that even if Mallory removes a bunch of carefully-selected vertices, there is still a path with a lot of key edges.

Depth-robust graphs: A depth-robust graph (DRG) is a DAG with almost exactly this property: even if a (potentially sizable) fraction of the vertices are removed, it retains a long path. This is a very useful property. Even if Mallory stores a lot of data, she can't remove all of the long paths. Ben Fisch first suggested applying this insight to PoReps in a manner similar to how Mahmoody et al. applied it to prove inherently sequential work.

The obvious way to build a PIE using a DRG is to cut the file into one piece per vertex and then scramble it one vertex at a time. The edges of the DRG become key edges, so the output of one vertex is needed (along with the relevant file block) to compute the next. Now, if Mallory throws away too much of the file, there will be a long path left in the DRG and she'll have to do a lot of sequential work to recompute the discarded data.

Unfortunately, this doesn't quite solve our problem. Mallory will need a lot of sequential work to recompute some of the discarded data, but not all of it. Some pieces will be easy to encode. Mallory can simply not store those pieces, instead opting to re-encode them on-the-fly. The first vertex in the path, for example, needs only one call to KDF.

In talks on possible approaches in early 2018, Fisch proposed this approach and suggested addressing this concern using erasure coding, making the file internally redundant. The idea was that at least some of the redundancy would be hard to re-encode. That approach, however, has several downsides. First, it expands the size of the file, potentially substantially. Second, it still allows cheating servers to gain some storage advantage over honest ones since they can discard some of the redundant data. This is a practical problem if storage providers are compensated for the full size of the expanded file. Finally, because each encoded block is required to recover not only its own plaintext but that of each of its children in the DRG, there was no clear technique for detecting a server that discarded enough data to make the file unrecoverable, nor a formal definition of what that would mean. [1]

We opted for a different, and we believe cleaner, approach. We want to force Mallory to do a long sequential computation for any block of data she's thrown away. Ensuring this while providing ASIC resistance is the critical challenge that any solution must confront.

Dagwood Sandwich Graphs (DSaGs)

The approach we take involves feeding the outputs of a depth-robust graph into a second type of graph called butterfly graph, which has the property that there's a path from every input node to every output node. This graph, with its dependency of every output on every input, helps ensure, roughly speaking, that Mallory must compute every input node, and therefore cannot avoid computing along the long sequential path in the depth-robust graph. In actual fact, to ensure this dependency, we must layer a sequence of depth-robust graphs and butterfly graphs, something like this (where the Gs are depth-robust graphs and the Bs are butterfly graphs):

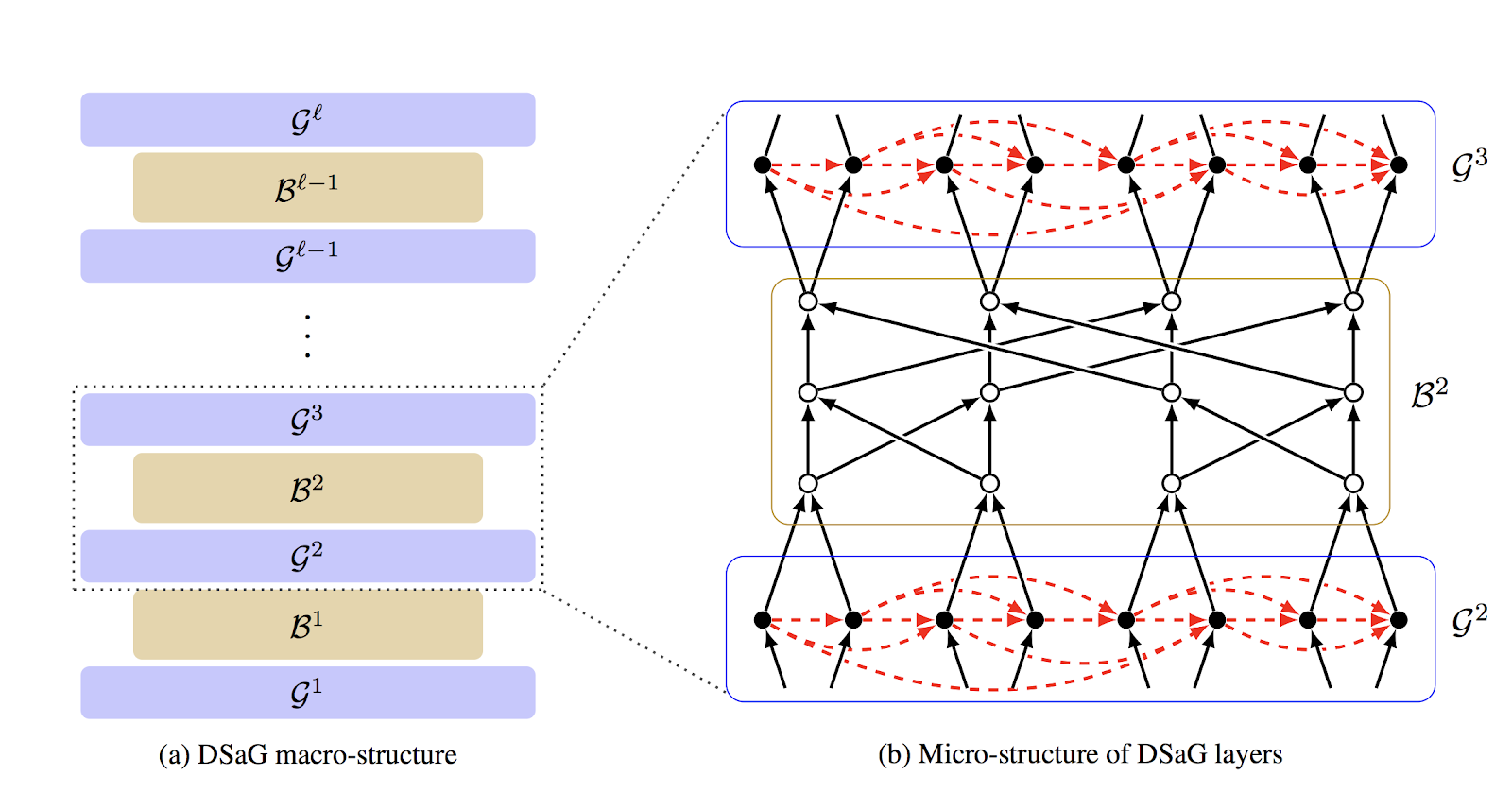
We think this construction looks like the famous Dagwood sandwiches from the cartoon strip Blondie, dramatized by the following lunch:

Yes, indeed. As if things weren't confusing enough, our PIE is made from a terrifying sandwich.

From PIE to DSN

Given a PIE, a potentially malicious storage provider like Mallory can prove that she's honestly replicating files. But how do you build a DSN using a PIE?

Pretty much any PIE-based DSN architecture involves two steps for a given file:

1. Prove once that the file is encoded correctly.
2. Audit by verifying continuously that the file is intact.

Let's start with (1). Storage providers in the DSN must prove to somebody—the file owner or the network—that an encoding G of a file F is a correct PIE. Given an authenticated version of F, such as a hash stored in a trusted place, it's easy to verify that a PIE is correct. It is public, after all, so anyone can decode G to recover F. Decoding is an expensive operation, though, so it would be nice to have an efficient way to prove correctness. We propose a different approach in our work, showing how to efficiently prove that G is incorrect. This creates conditions for various "cryptoeconomic" approaches to verification, such as slashing a provider proven to be cheating. Alternatively, SNARKs offer efficient means to verify, if not prove, correctness.

As for (2), it's not much help for G to be correct if it goes missing. It's critical to continuously check that storage providers are still storing G and haven't thrown data away. There are a number of efficient, well established techniques for this purpose. A simple one used by existing DSNs is to build a Merkle tree on G whose leaves are G's blocks and publish the root. A storage provider can then be challenged to provide a random leaf and prove its correctness by furnishing a path to the published root.

A blockchain can then perform the auditing. This could be an existing blockchain like Ethereum or, as with schemes like Sia, a new one whose consensus algorithm is independent of its storage goals. A particularly intriguing option, though, is to create a new blockchain where audit = mining.

The allure is an escape from the waste and environmental destruction of Proof of Work (PoW). Mining via useful storage was first proposed in 2014 in Permacoin. Permacoin required that nodes store a large, predetermined, public archive, however, and was only slightly less wasteful than conventional PoW.

PIEs completely change the game. Because they are incompressible, we eliminate any clever tricks a malicious miner could pull by specially crafting the files. Even if the file is all zeros, the miner must store the full encoded version. PIEs enable use of any files, even those owned by miners themselves, for mining = audit. This is the idea proposed in Filecoin, for example. Ultimately, PIEs may enable a secure and efficient consensus protocol whose main resource is storage devoted useful data, rather than wasted electricity. Provably secure, efficient PIEs are a first step in this direction, and parallel work by other teams happily promises to provide a stable of complementary, evolving techniques.

Creating a provably secure and minimal-waste scheme for mining = audit is the next step. IC3 is beavering away at it. We're happy to hear from partners who'd like to help create the next generation of DSN.

A full copy of this work can be found on the IACR Cryptology ePrint Archive.

Backstory and Acknowledgements

We would like to give a special thanks to Ben Fisch and Joe Bonneau for alerting us to the utility of depth-robust graphs. We had been working concurrently on the proof of replication problem initially using an approach based on hourglass functions, and butterfly graphs. We had several approaches that looked promising but, when we tried to prove them secure, turned out to be subtly but completely broken. We learned an important lesson: This problem space is deceptively hard. We therefore chose to hold off talking about results until we had a concrete construction and security proof. Only now have we gotten there.

After Ben's January 2018 talk on their approach, we had very useful discussions with both Ben and Joe about what security they could potentially achieve. This communication helped us identify the need for strong definitions that neither allowed a cheating server to discard any of the file risk-free nor required file expansion. It was not clear, though, how to adapt the construction Ben presented—effectively the strawman DRG construction given earlier in this post—to satisfy these properties. We got the idea of using depth-robust graphs in a different manner, combining them with hourglass functions. It took some time and very different definitions, but we ultimately arrived at a solution that provably achieved our desired properties.

We would also like to thank Juan Benet and Nicola Greco at Protocol Labs for helping clarify the motivation and practical requirements of the context.

Footnotes