Miner frontrunning is a fundamental problem in blockchain-based markets in which miners reorder, censor, and/or insert their own transactions to directly profit from markets running on blockchain economic mechanisms. Miner frontrunning takes advantage of the responsibility of miners in a blockchain system to order transactions in an attack described in great detail by Martin Swende in a blog post, which we highly recommend for background on this important issue.
Frontrunning is not strictly theoretical: in practice, frontrunning-like tactics have been observed during large ICO releases, with increasingly sophisticated attacks anticipated as the financial incentives for gaming high-profile contracts increase and attract more sophisticated attackers.
As described in a previous article on frontrunning, "any scheme that a) provides full information to miners b) doesn't include nondeterminism and c) is vulnerable to ordering dependencies is gameable."
In this article, we will examine a potential mitigating strategy for frontrunning through the lens of a fair sealed/closed bid auction mechanism that resists miner frontrunning. This strategy can be used for fair markets, fair ICOs, fair ENS-style auctions, and much more.
We stumbled upon this problem during the creation of our upcoming billion-dollar ICO token launch, HaxorBux (HXR).
Our mitigating strategy is an idea that we call a submarine send. Submarine sends aim at a strong confidentiality property. Rather than just concealing transaction amounts—which isn’t sufficient to prevent frontrunning, as we’ll show—submarine sends conceal the very existence of a transaction. Of course, a permanently concealed transaction isn’t very useful. Submarine sends thus also permit a transaction to be surfaced by the sender at any desired time in the future—thus the term “submarine”.
Submarines: They can’t frontrun you if they can’t find you
We have published a proof-of-concept implementation on github (still lacking some features like the Merkle-Patricia verification described later in this post). We encourage contributions and comments in the issues section there!
A folklore method for concealing transaction values—used for everything from randomness generation to (non-blockchain) sealed-bid auctions—is called commit / reveal. The idea is simple. In a first protocol phase, every user Ui submits a cryptographic commitment Ui = commit(vali) to the value vali representing her input to the protocol, e.g., her bid in an auction. After all inputs have been gathered, in a second phase, every player reveals vali by decommitting Ui. During the first, commitment phase, no user can see any other user’s bid / value vali and thus front-run the second phase.
This is all well and good, but vali is a value, not actual money. So what if a user wins a sealed-bid auction conducted this way. How do we ensure that she actually pays the amount val that she bid?
In a decentralized system, where users may be untrustworthy, val is a more or less worthless IOU. The only way to ensure payment is for all users actually to commit $val, i.e., commit the money represented in their bid. In Ethereum, though, there is no (simple [1]) way to conceal the amount of Ether in an ordinary send. So when P sends $val as a commitment, she reveals her bid amount. That brings us back to square one. [2]
Suppose instead of Ethereum, we were using a hypothetical system that actually concealed transaction amounts and even the sender identity (but not whether a contract receives a transaction). Call it ZEthereum. Then, of course, we’d solve the problem. Front running isn’t possible in an auction if you don’t know your competitors’ transaction amounts. Right?
Unfortunately, even concealed transaction amounts don’t do the trick, as a simple example shows.
Example 1 (Transaction Existence): Tweedledum is bidding on a rare military helmet in an auction administered through a ZEthereum smart contract. He knows that there is only one other possible bidder, his brother Tweedledee, who loves the helmet, but has at most $1000 available to bid for it. If Tweedledum learns of the existence of a second bid, his strategy is clear: He should bid $1000.01. Otherwise, he can win with a bid of $0.01, far below the real value of the helmet. Even though bid amounts are concealed, Tweedledum can game the auction by learning whether or not a bid exists.
Tweedledee cheated of helmet by Tweedledum’s frontrunning
While this example is contrived, there are real systems in which the existence and also the timing of bids can leak information. For instance, in an ICO, it’s easy to imagine even naive algorithms estimating interest in a token and altering their bid based on contract buy-in statistics.
Our solution, a submarine send, is a poor-man’s solution to the problem of concealing transaction amounts and existence for a target smart contract "Contract". It doesn’t conceal transaction amounts as strongly as our hypothetical ZEthereum would, and it doesn’t definitively hide the existence of transactions. But it provides what we believe to be good enough guarantees in many cases.
The key idea is to conceal sends to Contract among other, unrelated and indistinguishable transactions.
A submarine send embeds a real transaction among a collection of cover transactions, thus achieving a form of k-anonymity. Put another way, the submarine transaction sits in an anonymity set consisting of k cover transactions. While not as strong as notions such as differential privacy or full concealment based on cryptographic hardness assumptions, k-anonymity has proven useful in many practical settings. And some low-cost enhancements can strengthen our scheme’s properties.
The basic format of a submarine send is simple: It is a send of $val from an addrP, where P is the player interacting with Contract, to a fresh address addrX. The trick is to structure address addrX such that it has two properties: (1) addrX looks random in the view of potential adversaries and (2) $val is committed to SC in a manner that can be proven cryptographically.
Let’s illustrate with an example, showing how a system that is vulnerable to frontrunning can be rendered more secure by use of submarine sends.
Example 2 (Ash ICO): Suppose that smart contract AshContract implements sales of a new type of token called an Ash. Purchasers burn Ether to obtain tokens at a market-driven Ether-to-Ash exchange rate.
It’s easy to see that AshContract is vulnerable to frontrunning. A large buy transaction will substantially raise the market price of Ash. Thus a miner that observes such a transaction Trans can profit by squeezing in her own buy transaction before Trans and selling afterward. We can remedy this problem by enhancing AshContract as follows:
Example 2 (Ash ICO) continued: In a commit phase, a player P with address addrP makes a submarine send via transaction Trans as follows. P sends $val to address addrX for public key X, where X = H(addrP, SCN, TKEY), where SCN is a contract-specific identifier, TKEY is a transaction-specific key / witness (e.g., a randomly selected 256-bit value), and H is Ethereum-SHA-3.
In a reveal phase, to prove that she has burned $val, P sends TKEY to AshContract. AshContract then: (1) Verifies TKEY is a fresh key; (2) Computes X = H(addrP, SCN, TKEY) and addrX; and (3) Checks addrX.balance == $val. Upon successful verification, AshContract awards Ash tokens to P.
Observe that during the commit phase, X and addrX are computed from an as-yet unrevealed key (namely TKEY). Thus the transaction Trans is indistinguishable from an ordinary send to a fresh address. [3] Assuming that many other such ordinary sends happen during the bidding period, an adversary cannot identify Trans as a purchase of Ash.
During the reveal phase, P proves to AshContract that she burned $val to purchase Ash. [4] Given the way public key X is computed, it is infeasible to compute a corresponding valid private key. Thus money sent to addrX is unrecoverable, i.e., burned.
Of course, there are cases in which we don’t want to burn the committed currency. As we now show, it is possible to implement submarine sends in which $val is recoverable by AshContract after the reveal phase.
The two phases of a submarine send
It is possible to implement cheap and simple submarine sends in which $val can be recovered. For this purpose, we rely on a new feature introduced in EIP-86. EIP-86 was scheduled to go live in the upcoming Metropolis hard-fork, but unfortunately its deployment has been postponed for now. We detail a temporary, more expensive option for implementing submarine sends in the blog appendix.
The crucial change in EIP-86 is the introduction of a new CREATE2 opcode to the Ethereum Virtual Machine. Like the already existing CREATE opcode, the new opcode will also create new smart contracts on the blockchain. However, unlike CREATE, CREATE2 will compute the address of the newly created smart contract C as H(addrCreator, salt, codeC), where addrCreator is the address of the contract’s creator, salt is a 256-bit salt value chosen by the creator, and codeC is the EVM byte code of C’s initcode.
To construct submarine sends, we combine this new way of computing contract addresses with a very simple smart contract which we call Forwarder. Forwarder performs one function: Upon receiving a message-call, it checks whether the message-call was sent by Contract. If so, Forwarder sends its entire Ether balance to Contract. Otherwise, Forwarder does nothing. Here is a simple implementation of Forwarder written in Solidity:
contract Forwarder { address constant addrContract = 0x123; function () { if (msg.sender == addrContract) addrContract.send(this.balance); } }
To save gas, we can also implement Forwarder directly in EVM bytecode, reducing the size of the Forwarder contract by ~ 75%.
Let’s put the pieces together and examine how the commit and reveal phases work.
While EIP-86 offers the best vehicle for implementation of submarine sends, as noted above, it is nonetheless possible to implement them in Ethereum today. For details, see the blog appendix (“Submarine sends, today”.)
The astute reader might notice that an important step is still missing in the above scheme: Contract does not check that the transaction that sent $val to A actually happened during the commit phase! This is crucial, as otherwise we face a frontrunning issue again: Upon seeing a reveal of a submarine send, a miner could compute A, observe A.balance, and include his own commit and reveal transactions after the commitment phase has already ended.
So how should we go about verifying the timeliness of the transaction to A? The conceptually simplest solution is to verify this off-chain, e.g. using Etherscan, but that sort of defeats the purpose of smart contracts, right?
A more technically involved solution would be for P to reveal, in addition to Data, a proof that a transaction of $val to A was made during the commit phase. This proof can then be verified by Contract. The proof would include a block number, all the transaction’s attributes (transaction index, nonce, to, gasprice, value, etc), a Merkle-Patricia Proof of inclusion in the transaction trie, as well as a block header, and convince Contract that (1) that block was mined during the commit phase; and (2) that the relevant transaction is included in that block. However, generating and verifying such a proof for every submarine send is cumbersome and expensive.
The solution we propose follows an alternative “optimistic” approach: Instead of having every bidder prove to Contract that they followed the protocol correctly, we will allow parties to prove to Contract that some bidder cheated. As the cheating party will forfeit its bid as a result, this solution should incentivize correct behavior of the bidding parties. Bidders still reveal all transaction attributes and the corresponding block header to Contract but they do not include a proof (this is the expensive part after all). After the reveal phase is over, Contract enters a short verification phase in which parties may submit proofs that some other party’s reveal is incorrect. Analogously to the above proof of correct behavior, a proof of cheat consists in showing that the transaction attributes and block header revealed by a bidder are incorrect: i.e., that the given block is not in the blockchain, or that it does not contain the purported transaction. [5] If the proof verifies, Contract would collect the bid from the Forwarder contract, and send it to the loyal watchdog as reward. As verifying other bidders’ reveals off-chain is very simple, honest bidders have a strong incentive to check for and report a cheating party that outbid them (as long as honest bids are larger than the gas cost of proving wrongdoing).
We believe this solution offers a good compromise: Although Contract still has to implement the rather tedious procedure of verifying the (non-) inclusion of a transaction in Ethereum’s blockchain, this procedure should only ever be called if a party actually reveals an incorrect bid. In such a case, the misbehaving party’s bid is forfeited and used to offload the gas costs of the party that revealed the wrongdoing.
If we were to make a submarine send today, how hard would it be for a frontrunning miner to detect it? The answer to this question crucially depends on the size of the anonymity set we are trying to hide our submarine in. As a reminder, this anonymity set comprises other “normal” transactions in the Ethereum network that look the same as a submarine send.
Suppose our commit window spans blocks Bstart to Bend. During that window, a frontrunner will be looking for transactions to some address A that satisfy the following properties:
Such addresses A, which we refer to as “fresh addresses”, are candidates for being the destination of a submarine send and thus make up our anonymity set. Note that it is irrelevant whether these fresh addresses are involved in further transactions after the end of the commit window (i.e., in blocks after Bend). Indeed, although this could reveal that some addresses were actually not used as part of a submarine send (thus effectively reducing the anonymity set), at that point in time the danger of a frontrun is moot as the commit phase has passed.
The choice of the commit window (the number of blocks from Bstart to Bend) should thus be primarily governed by the size of the anonymity set one might expect over that period.
We performed a simple experiment to determine the effective size of the anonymity set for submarine sends. We selected a commit window of roughly 30 minutes between blocks 4007900 and 4008000. In that period, we recorded 7109 transactions (excluding internal transactions), of which 661 satisfy the above properties and thus make up an anonymity set for submarine sends.
As an example, consider this address which received 5 ETH in block 4007963 and has not been involved in any other transaction since. [7]
The graph below shows how the size of the anonymity set grows throughout the commit phase.
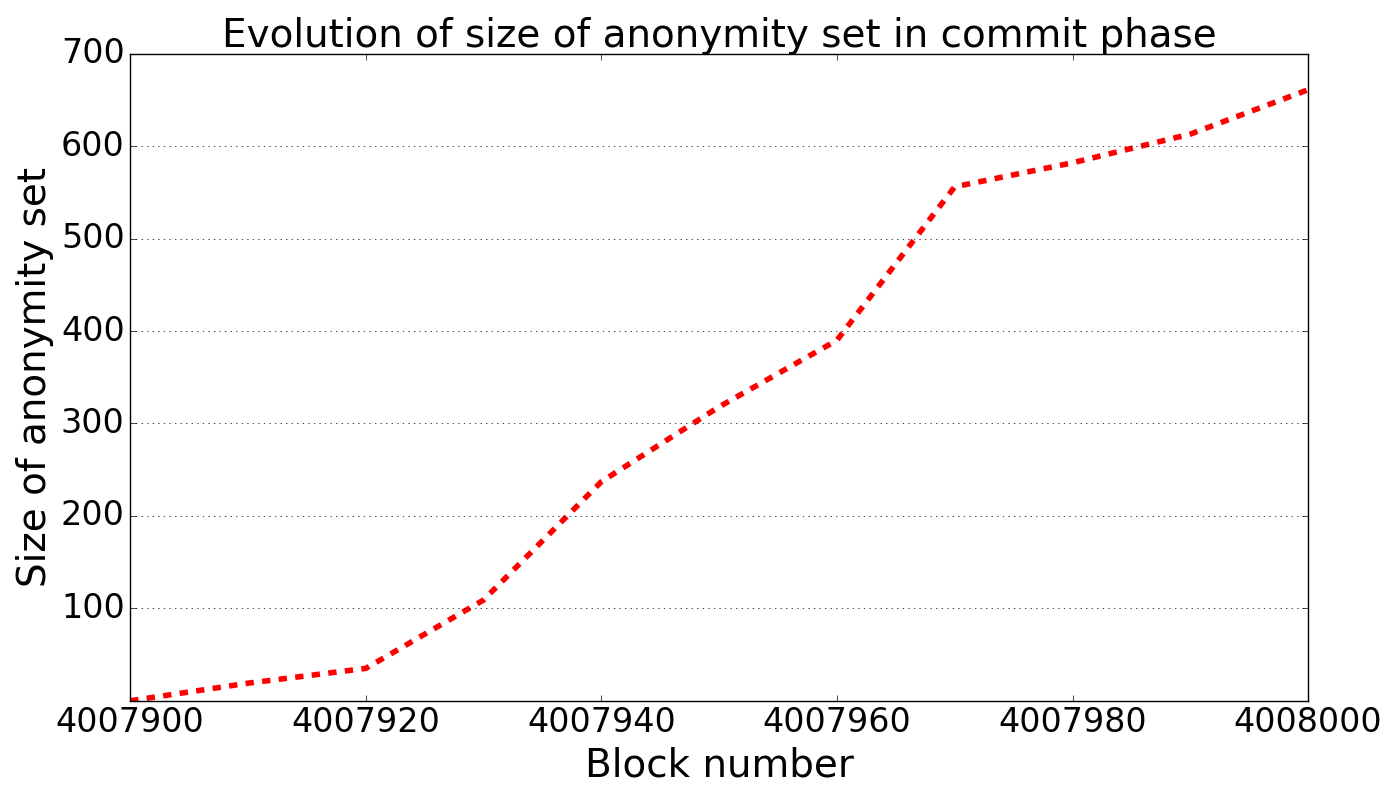
Size of anonymity set over time
If we consider a larger commit window of a little over two hours, between blocks 4007600 and 4008000, we find that the anonymity set for submarine sends consists of 1534 “fresh” addresses.
Of course, a frontrunning miner might try to use information other than the freshness of the destination address to de-anonymize a submarine send. In particular, perhaps the miner knows that the transaction she wants to frontrun will contain a certain amount of Ether. In that case, it is important that the submarine send “blends in” with other transactions of similar value. Thus effective cover transactions must also contain transaction amounts that are statistically similar to that in the submarine send.
Fortunately, we found that the transactions that make the anonymity set span a diverse range of Ether amounts, with the majority of values between 0.01 and 100 ETH, and an average transaction value of about 6 ETH. Below we show the distribution of Ether values for the transactions to fresh addresses between blocks 4007900 and 4008000.
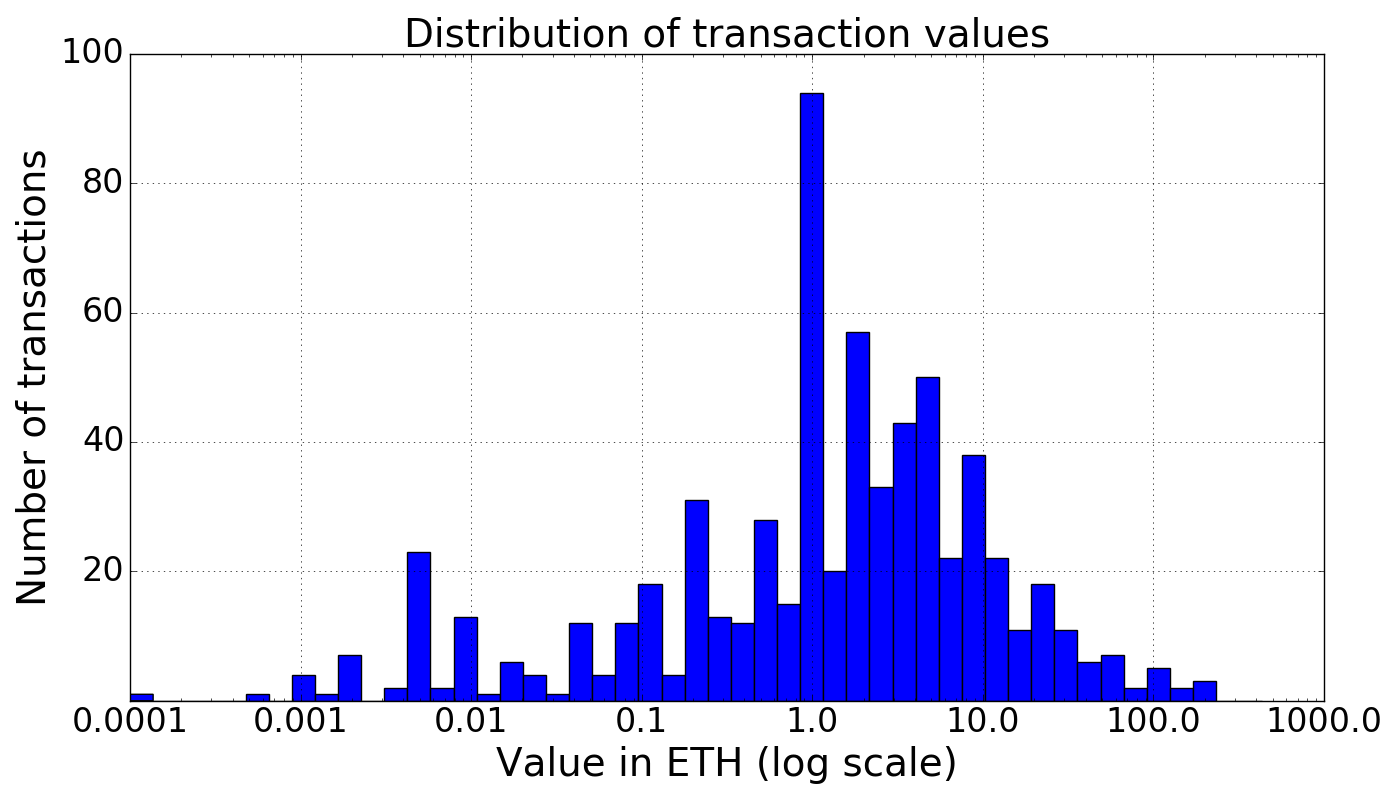
Transaction value histogram, blocks 4007900 to 4008000
Furthermore, there are a few ways to perform what we call transaction shaping in order to help prevent transaction amounts from revealing submarine sends:
Frontrunning and related problems are pervasive problems, with no good available remedies in Ethereum. Submarine sends, while imperfect, offer a powerful and practical solution. Fortunately, there is already a fairly high volume of low-to-medium-value cover transactions in Ethereum today, and we can expect it to grow as the system evolves. Our proof-of-concept works on the Ethereum network today, though it costs more gas than our ideal scheme. For submarine sends to be truly practical, all we await is the adoption of EIP-86.
If you don’t want to wait until EIP-86 is adopted, we have good news for you. It is already possible to use Submarine Sends in Ethereum, although it is more complex and costly than in the future EIP-86-Ethereum. To rid ourselves of the dependency on EIP-86, we need another way to construct fresh addresses that are later inhabited by a contract. Since we cannot use CREATE2, we will have to make do with CREATE.
Whenever a contract is created with CREATE, its address is computed as H(addrCreator, nonceCreator), where addrCreator is the address of the contract’s creator and nonceCreator counts how many contracts have been created by the contract’s creator. [8] Hence, the creator has some control over nonceCreator: to increment nonceCreator by one, the creator only has to spawn a new contract. Of course, incrementing nonceCreator until it encodes the output of a cryptographic hash function (say 80 bits [9]) is completely out of the question. But we can encode this value in a series of nonces, making the scheme somewhat practical.
As in the EIP-86 example, we also need a Forwarder contract. However, Forwarder isn’t quite as simple as in the EIP-86 example; beyond forwarding funds to Contract, it now also must be able to clone itself, i.e. to CREATE a new instance of itself.
Once again, we have a commit and a reveal phase:
We have created a prototype implementation using 80 bits for H’(Data) in which creating a series of contracts and withdrawing the funds costs ~5 million gas. [11] We believe that optimising this implementation would bring the gas cost down by roughly 50%. At a currently feasible gas price of 4 gigawei this corresponds to 0.02 ETH or 3.65 USD.
Of course, our scheme has some limitations. Attacks still exist where an adversary can spam a large volume of high-fee transactions in an attempt to stop players from either committing or revealing, especially late in these periods. The longer the period, the more costly this becomes to the adversary. One mitigation strategy is to make the period long enough that the cost required to fill blocks exceeds the value estimated to be at stake.
Unfortunately, an inherent tradeoff between latency and fairness may always exist in systems aiming to provide fairness guarantees by tackling frontrunning, as smaller periods of hiding information from miners leave users more vulnerable to reorganizations and consider the input of fewer miners.
| [1] | https://blog.ethereum.org/2017/01/19/update-integrating-zcash-ethereum/ |
| [2] | There are other approaches to addressing front-running that don’t involve concealment of transaction amounts: (A) Players could commit small, uniformly priced deposits that they forfeit if they fail to pay. But they may still not be incentivized to pay in full. (B) Players can break up their bids across multiple transactions and reveal their belonging to the same bid in the reveal phase. But a lack of transaction-graph confidentiality means that even bids from multiple addresses might be tied to the same user. We propose this approach as an added layer of security for submarine sends, but its limitations need to be made clear. |
| [3] | Indeed, in the Random Oracle Model, the ability to identify Trans as a submarine send would imply the ability to perform signature forgery. |
| [4] | This example glosses over the details of how party P convinces Contract that the burn of $val actually occurred during the commit phase and not after. We’ll come back to this important issue in the next section. |
| [5] | As the Transaction Trie is sorted, showing that a transaction is not in it simply reduces to showing that either there is no transaction with the given index in the trie or that the transaction at the given transaction index has different attributes than the ones given during the reveal. |
| [6] | If the address only receives transactions, it could technically still be a candidate for a submarine send as we could always split up a submarine send into multiple transactions to the same destination address. |
| [7] | At the time of writing, the most recent block number is 4036411. |
| [8] | This isn’t the whole story: If the creator is a contract, nonceCreator counts how many contracts have been created by the creator. Otherwise, nonceCreator counts how many transactions have been initiated by the creator. Furthermore, the inputs to the hash function are rlp-encoded before hashing. |
| [9] | Since we don’t require our hash function to be resistant to collision attacks, we don’t have to worry about the birthday paradox and can get away with using a shorter hash. 80 bits should still provide ample defense against pre-image attacks, especially in light of the fact that an attacker only has a rather short amount of time in which finding a pre-image benefits her. |
| [10] | Somewhat surprisingly, a theoretical analysis reveals that out of all fixed-width chunking schemes, 2-bit chunking is the cheapest on average. For example, using 2-bit chunks is 20% more efficient than using 1-bit chunks. |
| [11] | Since this comes close to the block gas limit, we split the withdrawal process into multiple transactions. Note that it’s relatively cheap to compute A; the high gas cost is caused by the creation of the hundreds of contracts needed for withdrawing funds from A. |
Lorenz (lorenzb.com) is an SNF BRIDGE fellow in the group of Srdjan Capkun at ETH Zürich. Previously, Lorenz did research at Cornell Tech under the supervision of Ari Juels. more...
Ari Juels is a Professor at the Jacobs Technion-Cornell Institute at Cornell Tech in NYC and Co-Director of IC3. more...
bitcoin / security / ethereum / hyperdex / release / nosql / selfish-mining / blocksize / dao / surveillance / privacy / mongo / broken / weaver / nsa / meta / leveldb / blockchain / 51% / voting / smart contracts / graph stores / decentralization / bitcoin-ng / vaults / snowden / satoshi / philosophy / mt. gox / mining pools
